Welcome to the Algebra worksheets page at Math-Drills.com, where unknowns are common and variables are the norm. On this page, you will find Algebra worksheets for middle school students on topics such as algebraic expressions, equations and graphing functions.
This page starts off with some missing numbers worksheets for younger students. We then get right into algebra by helping students recognize and understand the basic language related to algebra. The rest of the page covers some of the main topics you'll encounter in algebra units. Remember that by teaching students algebra, you are helping to create the future financial whizzes, engineers, and scientists that will solve all of our world's problems.
Algebra is much more interesting when things are more real. Solving linear equations is much more fun with a two pan balance, some mystery bags and a bunch of jelly beans. Algebra tiles are used by many teachers to help students understand a variety of algebra topics. And there is nothing like a set of co-ordinate axes to solve systems of linear equations.
Most Popular Algebra Worksheets this Week





Algebraic Properties, Rules and Laws Worksheets

The commutative law or commutative property states that you can change the order of the numbers in an arithmetic problem and still get the same results. In the context of arithmetic, it only works with addition or multiplication operations, but not mixed addition and multiplication. For example, 3 + 5 = 5 + 3 and 9 × 5 = 5 × 9. A fun activity that you can use in the classroom is to brainstorm non-numerical things from everyday life that are commutative and non-commutative. Putting on socks, for example, is commutative because you can put on the right sock then the left sock or you can put on the left sock then the right sock and you will end up with the same result. Putting on underwear and pants, however, is non-commutative.
The associative law or associative property allows you to change the grouping of the operations in an arithmetic problem with two or more steps without changing the result. The order of the numbers stays the same in the associative law. As with the commutative law, it applies to addition-only or multiplication-only problems. It is best thought of in the context of order of operations as it requires that parentheses must be dealt with first. An example of the associative law is: (9 + 5) + 6 = 9 + (5 + 6). In this case, it doesn't matter if you add 9 + 5 first or 5 + 6 first, you will end up with the same result. Students might think of some examples from their experience such as putting items on a tray at lunch. They could put the milk and vegetables on their tray first then the sandwich or they could start with the vegetables and sandwich then put on the milk. If their tray looks the same both times, they will have modeled the associative law. Reading a book could be argued as either associative or nonassociative as one could potentially read the final chapters first and still understand the book as well as someone who read the book the normal way.
Inverse relationships worksheets cover a pre-algebra skill meant to help students understand the relationship between multiplication and division and the relationship between addition and subtraction.
-
Addition and Subtraction Easy Addition and Subtraction Harder All Multiplication and Division Facts 1 to 18 in color (no blanks) Multiplication and Division Range 1 to 9 Multiplication and Division Range 5 to 12 Multiplication and Division All Inverse Relationships Range 2 to 9 Multiplication and Division All Inverse Relationships Range 5 to 12 Multiplication and Division All Inverse Relationships Range 10 to 25
-
Addition and Subtraction (Sums 1-18) Addition and Subtraction Inverse Relationships with 1 Addition and Subtraction Inverse Relationships with 2 Addition and Subtraction Inverse Relationships with 3 Addition and Subtraction Inverse Relationships with 4 Addition and Subtraction Inverse Relationships with 5 Addition and Subtraction Inverse Relationships with 6 Addition and Subtraction Inverse Relationships with 7 Addition and Subtraction Inverse Relationships with 8 Addition and Subtraction Inverse Relationships with 9 Addition and Subtraction Inverse Relationships with 10 Addition and Subtraction Inverse Relationships with 11 Addition and Subtraction Inverse Relationships with 12 Addition and Subtraction Inverse Relationships with 13 Addition and Subtraction Inverse Relationships with 14 Addition and Subtraction Inverse Relationships with 15 Addition and Subtraction Inverse Relationships with 16 Addition and Subtraction Inverse Relationships with 17 Addition and Subtraction Inverse Relationships with 18
The distributive property is an important skill to have in algebra. In simple terms, it means that you can split one of the factors in multiplication into addends, multiply each addend separately, add the results, and you will end up with the same answer. It is also useful in mental math, an example of which should help illustrate the definition. Consider the question, 35 × 12. Splitting the 12 into 10 + 2 gives us an opportunity to complete the question mentally using the distributive property. First multiply 35 × 10 to get 350. Second, multiply 35 × 2 to get 70. Lastly, add 350 + 70 to get 420. In algebra, the distributive property becomes useful in cases where one cannot easily add the other factor before multiplying. For example, in the expression, 3(x + 5), x + 5 cannot be added without knowing the value of x. Instead, the distributive property can be used to multiply 3 × x and 3 × 5 to get 3x + 15.
Students should be able to substitute known values in for an unknown(s) in an expression and evaluate the expression's value.
-
Evaluating Expressions with One Variable, One Step and No Exponents Evaluating Expressions with One Variable and One Step Evaluating Expressions with One Variable and Two Steps Evaluating Expressions with Up to Two Variables and Two Steps Evaluating Expressions with Up to Two Variables and Three Steps Evaluating Expressions with Up to Three Variables and Four Steps Evaluating Expressions with Up to Three Variables and Five Steps
As the title says, these worksheets include only basic exponent rules questions. Each question only has two exponents to deal with; complicated mixed up terms and things that a more advanced student might work out are left alone. For example, 42 is (22)2 = 24, but these worksheets just leave it as 42, so students can focus on learning how to multiply and divide exponents more or less in isolation.
-
Mixed Exponent Rules (All Positive) Mixed Exponent Rules (With Negatives) Multiplying Exponents (All Positive) Multiplying Exponents (With Negatives) Multiplying the Same Exponent with Different Bases (All Positive) Multiplying the Same Exponent with Different Bases (With Negatives) Dividing Exponents with a Greater Exponent in Dividend (All Positive) Dividing Exponents with a Greater Exponent in Dividend (With Negatives) Dividing Exponents with a Greater Exponent in Divisor (All Positive) Dividing Exponents with a Greater Exponent in Divisor (With Negatives) Powers of Exponents (All Positive) Powers of Exponents (With Negatives)
Knowing the language of algebra can help to extract meaning from word problems and to situations outside of school. In these worksheets, students are challenged to convert phrases into algebraic expressions.
Combining like terms is something that happens a lot in algebra. Students can be introduced to the topic and practice a bit with these worksheets. The bar is raised with the adding and subtracting versions that introduce parentheses into the expressions. For students who have a good grasp of fractions, simplifying simple algebraic fractions worksheets present a bit of a challenge over the other worksheets in this section.
-
Adding and simplifying linear expressions Adding and simplifying linear expressions with multipliers Adding and simplifying linear expressions with some multipliers. Subtracting and simplifying linear expressions Subtracting and simplifying linear expressions with multipliers Subtracting and simplifying linear expressions with some multipliers Mixed adding and subtracting and simplifying linear expressions Mixed adding and subtracting and simplifying linear expressions with multipliers Mixed adding and subtracting and simplifying linear expressions with some multipliers Simplify simple algebraic fractions (easier) Simplify simple algebraic fractions (harder)
Linear Expressions and Equations

In these worksheets, the unknown is limited to the question side of the equation which could be on the left or the right of equal sign.
-
Missing Numbers in Equations (All Operations; Range 1 to 9; Blanks Never in Answer Position) Missing Numbers in Equations (All Operations; Range 1 to 9; Blanks in Any Position) Missing Numbers in Equations (All Operations; Range 1 to 20; Blanks Never in Answer Position) Missing Numbers in Equations (All Operations; Range 1 to 20; Blanks in Any Position) Missing Numbers in Equations (Addition Only; Range 1 to 9; Blanks Never in Answer Position) Missing Numbers in Equations (Addition Only; Range 1 to 9; Blanks in Any Position) Missing Numbers in Equations (Addition Only; Range 1 to 20; Blanks in Any Position) Missing Numbers in Equations (Subtraction Only; Range 1 to 9; Blanks Never in Answer Position) Missing Numbers in Equations (Subtraction Only; Range 1 to 9; Blanks in Any Position) Missing Numbers in Equations (Subtraction Only; Range 1 to 20; Blanks in Any Position) Missing Numbers in Equations (Multiplication Only; Range 1 to 9; Blanks Never in Answer Position) Missing Numbers in Equations (Multiplication Only; Range 1 to 9; Blanks in Any Position) Missing Numbers in Equations (Multiplication Only; Range 1 to 20; Blanks in Any Position) Missing Numbers in Equations (Division Only; Range 1 to 9; Blanks Never in Answer Position) Missing Numbers in Equations (Division Only; Range 1 to 9; Blanks in Any Position) Missing Numbers in Equations (Division Only; Range 1 to 20; Blanks in Any Position)
-
Missing Numbers in Equations (All Operations; Range 1 to 9; Symbols Never in Answer Position) Missing Numbers in Equations (All Operations; Range 1 to 9; Symbols in Any Position) Missing Numbers in Equations (All Operations; Range 1 to 20; Symbols Never in Answer Position) Missing Numbers in Equations (All Operations; Range 1 to 20; Symbols in Any Position) Missing Numbers in Equations (Addition Only; Range 1 to 9; Symbols Never in Answer Position) Missing Numbers in Equations (Addition Only; Range 1 to 9; Symbols in Any Position) Missing Numbers in Equations (Addition Only; Range 1 to 20; Symbols in Any Position) Missing Numbers in Equations (Subtraction Only; Range 1 to 9; Symbols Never in Answer Position) Missing Numbers in Equations (Subtraction Only; Range 1 to 9; Symbols in Any Position) Missing Numbers in Equations (Subtraction Only; Range 1 to 20; Symbols in Any Position) Missing Numbers in Equations (Multiplication Only; Range 1 to 9; Symbols Never in Answer Position) Missing Numbers in Equations (Multiplication Only; Range 1 to 9; Symbols in Any Position) Missing Numbers in Equations (Multiplication Only; Range 1 to 20; Symbols in Any Position) Missing Numbers in Equations (Division Only; Range 1 to 9; Symbols Never in Answer Position) Missing Numbers in Equations (Division Only; Range 1 to 9; Symbols in Any Position) Missing Numbers in Equations (Division Only; Range 1 to 20; Symbols in Any Position)
-
Missing Numbers in Equations (All Operations; Range 1 to 9; Variables Never in Answer Position) Missing Numbers in Equations (All Operations; Range 1 to 9; Variables in Any Position) Missing Numbers in Equations (All Operations; Range 1 to 20; Variables Never in Answer Position) Missing Numbers in Equations (All Operations; Range 1 to 20; Variables in Any Position) Missing Numbers in Equations (Addition Only; Range 1 to 9; Variables Never in Answer Position) Missing Numbers in Equations (Addition Only; Range 1 to 9; Variables in Any Position) Missing Numbers in Equations (Addition Only; Range 1 to 20; Variables in Any Position) Missing Numbers in Equations (Subtraction Only; Range 1 to 9; Variables Never in Answer Position) Missing Numbers in Equations (Subtraction Only; Range 1 to 9; Variables in Any Position) Missing Numbers in Equations (Subtraction Only; Range 1 to 20; Variables in Any Position) Missing Numbers in Equations (Multiplication Only; Range 1 to 9; Variables Never in Answer Position) Missing Numbers in Equations (Multiplication Only; Range 1 to 9; Variables in Any Position) Missing Numbers in Equations (Multiplication Only; Range 1 to 20; Variables in Any Position) Missing Numbers in Equations (Division Only; Range 1 to 9; Variables Never in Answer Position) Missing Numbers in Equations (Division Only; Range 1 to 9; Variables in Any Position) Missing Numbers in Equations (Division Only; Range 1 to 20; Variables in Any Position)
-
Solving Simple Linear Equations with Values from -9 to 9 (Unknown on Left Side) Solving Simple Linear Equations with Values from -99 to 99 (Unknown on Left Side) Solving Simple Linear Equations with Values from -9 to 9 (Unknown on Right or Left Side) Solving Simple Linear Equations with Values from -99 to 99 (Unknown on Right or Left Side)
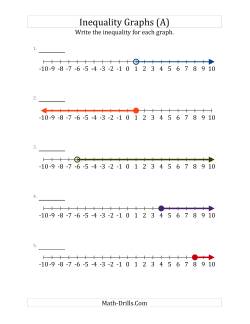
Graphing linear equations and reading existing graphs give students a visual representation that is very useful in understanding the concepts of slope and y-intercept.
-
Determine the Equation from a Graph Determine the Slope from a Graph Determine the y-intercept from a Graph Determine the x-intercept from a Graph Determine the slope and y-intercept from a Graph Determine the slope and intercepts from a Graph Determine the slope, intercepts and equation from a Graph
Solving linear equations with jelly beans is a fun activity to try with students first learning algebraic concepts. Ideally, you will want some opaque bags with no mass, but since that isn't quite possible (the no mass part), there is a bit of a condition here that will actually help students understand equations better. Any bags that you use have to be balanced on the other side of the equation with empty ones.
Probably the best way to illustrate this is through an example. Let's use 3x + 2 = 14. You may recognize the x as the unknown which is actually the number of jelly beans we put in each opaque bag. The 3 in the 3x means that we need three bags. It's best to fill the bags with the required number of jelly beans out of view of the students, so they actually have to solve the equation.
On one side of the two-pan balance, place the three bags with x jelly beans in each one and two loose jelly beans to represent the + 2 part of the equation. On the other side of the balance, place 14 jelly beans and three empty bags which you will note are required to "balance" the equation properly. Now comes the fun part... if students remove the two loose jelly beans from one side of the equation, things become unbalanced, so they need to remove two jelly beans from the other side of the balance to keep things even. Eating the jelly beans is optional. The goal is to isolate the bags on one side of the balance without any loose jelly beans while still balancing the equation.
The last step is to divide the loose jelly beans on one side of the equation into the same number of groups as there are bags. This will probably give you a good indication of how many jelly beans there are in each bag. If not, eat some and try again. Now, we realize this won't work for every linear equation as it is hard to have negative jelly beans, but it is another teaching strategy that you can use for algebra.
Despite all appearances, equations of the type a/x are not linear. Instead, they belong to a different kind of equations. They are good for combining them with linear equations, since they introduce the concept of valid and invalid answers for an equation (what will be later called the domain of a function). In this case, the invalid answers for equations in the form a/x, are those that make the denominator become 0.
-
Combining Like Terms and Solving Simple Linear Equations Solving ax = c Linear Equations Solving ax = c Linear Equations including negatives Solving x/a = c Linear Equations Solving x/a = c Linear Equations including negatives Solving a/x = c Linear Equations Solving a/x = c Linear Equations including negatives Solving ax + b = c Linear Equations Solving ax + b = c Linear Equations including negatives Solving ax - b = c Linear Equations Solving ax - b = c Linear Equations including negatives Solving ax ± b = c Linear Equations Solving ax ± b = c Linear Equations including negatives Solving x/a ± b = c Linear Equations Solving x/a ± b = c Linear Equations including negatives Solving a/x ± b = c Linear Equations Solving a/x ± b = c Linear Equations including negatives Solving various a/x ± b = c and x/a ± b = c Linear Equations Solving various a/x ± b = c and x/a ± b = c Linear Equations including negatives Solving linear equations of all types Solving linear equations of all types including negatives
Algebra rectangles are rectangles that use linear expressions for the side measurements. With a known value (such as the perimeter), students create an algebraic equation that they can solve to determine the value of the unknown (x) and use it to determine the side lengths and area of the rectangle. The terminology in identifying the various options for worksheets use the standard equation y = mx + b where m is the coeffient of x that is generally a known value.
-
Algebra Rectangles -- Determining the Value of x, Length, Width and Area Using Algebraic Sides and the Perimeter -- m Range [1,1] Algebra Worksheet -{}- Algebra Rectangles -- Determining the Value of x, Length, Width and Area Using Algebraic Sides and the Perimeter -- m Range [2,9] Algebra Worksheet -{}- Algebra Rectangles -- Determining the Value of x, Length, Width and Area Using Algebraic Sides and the Perimeter -- m Range [2,9] or [-9,-2] Algebra Worksheet -{}- Algebra Rectangles -- Determining the Value of x, Length, Width and Area Using Algebraic Sides and the Perimeter -- m Range [2,9] or [-9,-2] -- Inverse m Possible
Linear Systems

-
Easy Linear Systems with Two Variables Easy Linear Systems with Two Variables including negative values Linear Systems with Two Variables Linear Systems with Two Variables including negative values Easy Linear Systems with Three Variables; Easy Easy Linear Systems with Three Variables including negative values Linear Systems with Three Variables Linear Systems with Three Variables including negative values
-
Solve Linear Systems by Graphing (Solutions in first quadrant only) Solve Standard Linear Systems by Graphing Solve Slope-Intercept Linear Systems by Graphing Solve Various Linear Systems by Graphing Identify the Dependent Linear System by Graphing Identify the Inconsistent Linear System by Graphing
Quadratic Expressions and Equations
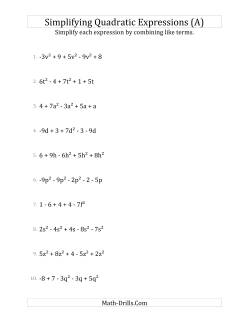
-
Simplifying quadratic expressions with 5 terms Simplifying quadratic expressions with 6 terms Simplifying quadratic expressions with 7 terms Simplifying quadratic expressions with 8 terms Simplifying quadratic expressions with 9 terms Simplifying quadratic expressions with 10 terms Simplifying quadratic expressions with 5 to 10 terms
-
Adding and simplifying quadratic expressions. Adding and simplifying quadratic expressions with multipliers. Adding and simplifying quadratic expressions with some multipliers. Subtracting and simplifying quadratic expressions. Subtracting and simplifying quadratic expressions with multipliers. Subtracting and simplifying quadratic expressions with some multipliers. Mixed adding and subtracting and simplifying quadratic expressions. Mixed adding and subtracting and simplifying quadratic expressions with multipliers. Mixed adding and subtracting and simplifying quadratic expressions with some multipliers.
-
Multiplying Factors of Quadratics with Coefficients of 1 Multiplying Factors of Quadratics with Coefficients of 1 or -1 Multiplying Factors of Quadratics with Coefficients of 1, or 2 Multiplying Factors of Quadratics with Coefficients of 1, -1, 2 or -2 Multiplying Factors of Quadratics with Coefficients up to 9 Multiplying Factors of Quadratics with Coefficients between -9 and 9
The factoring quadratic expressions worksheets in this section provide many practice questions for students to hone their factoring strategies. If you would rather worksheets with quadratic equations, please see the next section. These worksheets come in a variety of levels with the easier ones are at the beginning. The 'a' coefficients referred to below are the coefficients of the x2 term as in the general quadratic expression: ax2 + bx + c. There are also worksheets in this section for calculating sum and product and for determining the operands for sum and product pairs.
-
Factoring Quadratic Expressions with Positive 'a' coefficients of 1 Factoring Quadratic Expressions with Positive or Negative 'a' coefficients of 1 Factoring Quadratic Expressions with Positive or Negative 'a' coefficients of 1 with a Common Factor Step Factoring Quadratic Expressions with Positive 'a' coefficients up to 4 Factoring Quadratic Expressions with Positive or Negative 'a' coefficients up to 4 Factoring Quadratic Expressions with Positive or Negative 'a' coefficients up to 4 with a Common Factor Step Factoring Quadratic Expressions with Positive 'a' coefficients up to 5 Factoring Quadratic Expressions with Positive or Negative 'a' coefficients up to 5 Factoring Quadratic Expressions with Positive or Negative 'a' coefficients up to 5 with a Common Factor Step Factoring Quadratic Expressions with Positive 'a' coefficients up to 9 Factoring Quadratic Expressions with Positive or Negative 'a' coefficients up to 9 Factoring Quadratic Expressions with Positive or Negative 'a' coefficients up to 9 with a Common Factor Step Factoring Quadratic Expressions with Positive 'a' coefficients up to 81 Factoring Quadratic Expressions with Positive or Negative 'a' coefficients up to 81 Factoring Quadratic Expressions with Positive or Negative 'a' coefficients up to 81 with a Common Factor Step Calculating Sum and Product (Operand Range 0 to 9) ✎ Calculating Sum and Product (Operand Range 1 to 9) ✎ Calculating Sum and Product (Operand Range 0 to 9 Including Negatives) ✎ Calculating Sum and Product (Operand Range 1 to 9 Including Negatives) ✎ Calculating Sum and Product (Operand Range -20 to 20) ✎ Calculating Sum and Product (Operand Range -99 to 99) ✎ Determining Operands from Sum and Product Pairs (Operand Range 0 to 9) ✎ Determining Operands from Sum and Product Pairs (Operand Range 1 to 9) ✎ Determining Operands from Sum and Product Pairs (Operand Range 0 to 12) ✎ Determining Operands from Sum and Product Pairs (Operand Range 1 to 12) ✎ Determining Operands from Sum and Product Pairs (Operand Range 0 to 9 Including Negatives) ✎ Determining Operands from Sum and Product Pairs (Operand Range 1 to 9 Including Negatives) ✎ Determining Operands from Sum and Product Pairs (Operand Range -20 to 20) ✎ Determining Operands from Sum and Product Pairs (Operand Range -99 to 99) ✎
Whether you use trial and error, completing the square or the general quadratic formula, these worksheets include a plethora of practice questions with answers. In the first section, the worksheets include questions where the quadratic expressions equal 0. This makes the process similar to factoring quadratic expressions, with the additional step of finding the values for x when the expression is equal to 0. In the second section, the expressions are generally equal to something other than x, so there is an additional step at the beginning to make the quadratic expression equal zero.
-
Solving Quadratic Equations with Positive 'a' coefficients of 1 Solving Quadratic Equations with Positive or Negative 'a' coefficients of 1 Solving Quadratic Equations with Positive or Negative 'a' coefficients of 1 with a Common Factor Step Solving Quadratic Equations with Positive 'a' coefficients up to 4 Solving Quadratic Equations with Positive or Negative 'a' coefficients up to 4 Solving Quadratic Equations with Positive or Negative 'a' coefficients up to 4 with a Common Factor Step Solving Quadratic Equations with Positive 'a' coefficients up to 5 Solving Quadratic Equations with Positive or Negative 'a' coefficients up to 5 Solving Quadratic Equations with Positive or Negative 'a' coefficients up to 5 with a Common Factor Step Solving Quadratic Equations with Positive 'a' coefficients up to 9 Solving Quadratic Equations with Positive or Negative 'a' coefficients up to 9 Solving Quadratic Equations with Positive or Negative 'a' coefficients up to 9 with a Common Factor Step Solving Quadratic Equations with Positive 'a' coefficients up to 81 Solving Quadratic Equations with Positive or Negative 'a' coefficients up to 81 Solving Quadratic Equations with Positive or Negative 'a' coefficients up to 81 with a Common Factor Step
-
Solving Quadratic Equations for x ("a" coefficients of 1) Solving Quadratic Equations for x ("a" coefficients of 1 or -1) Solving Quadratic Equations for x ("a" coefficients up to 4) Solving Quadratic Equations for x ("a" coefficients between -4 and 4) Solving Quadratic Equations for x ("a" coefficients up to 81) Solving Quadratic Equations for x ("a" coefficients between -81 and 81)
Other Polynomial and Monomial Expressions & Equations

-
Factoring Non-Quadratic Expressions with No Squares, Simple Coefficients, and Positive Multipliers Factoring Non-Quadratic Expressions with No Squares, Simple Coefficients, and Negative and Positive Multipliers Factoring Non-Quadratic Expressions with No Squares, Compound Coefficients, and Positive Multipliers Factoring Non-Quadratic Expressions with No Squares, Compound Coefficients, and Negative and Positive Multipliers
-
Factoring Non-Quadratic Expressions with All Squares, Simple Coefficients, and Positive Multipliers Factoring Non-Quadratic Expressions with All Squares, Simple Coefficients, and Negative and Positive Multipliers Factoring Non-Quadratic Expressions with All Squares, Compound Coefficients, and Positive Multipliers Factoring Non-Quadratic Expressions with All Squares, Compound Coefficients, and Negative and Positive Multipliers
-
Factoring Non-Quadratic Expressions with Some Squares, Simple Coefficients, and Positive Multipliers Factoring Non-Quadratic Expressions with Some Squares, Simple Coefficients, and Negative and Positive Multipliers Factoring Non-Quadratic Expressions with Some Squares, Compound Coefficients, and Positive Multipliers Factoring Non-Quadratic Expressions with Some Squares, Compound Coefficients, and Negative and Positive Multipliers