Welcome to the fractions worksheets page at Math-Drills.com where the cup is half full! This is one of our more popular pages most likely because learning fractions is incredibly important in a person's life and it is a math topic that many approach with trepidation due to its bad rap over the years. Fractions really aren't that difficult to master especially with the support of our wide selection of worksheets.
This page includes Fractions worksheets for understanding fractions including modeling, comparing, ordering, simplifying and converting fractions and operations with fractions. We start you off with the obvious: modeling fractions. It is a great idea if students can actually understand what a fraction is, so please do spend some time with the modeling aspect. Relating modeling to real life helps a great deal too as it is much easier to relate to half a cookie than to half a square. Ask most students what you get if you add half a cookie and another half a cookie, and they'll probably let you know that it makes one delicious snack.
The other fractions worksheets on this page are devoted to helping students understand the concept of fractions. From comparing and ordering to simplifying and converting... by the time students master the material on this page, operations of fractions will be a walk in the park.
Most Popular Fractions Worksheets this Week





Fraction Circles
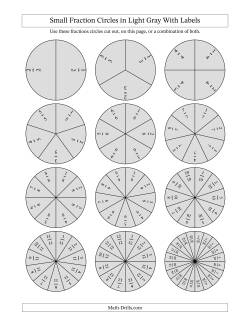
Fraction circle manipulatives are mainly used for comparing fractions, but they can be used for a variety of other purposes such as representing and identifying fractions, adding and subtracting fractions, and as probability spinners. There are a variety of options depending on your purpose. Fraction circles come in small and large versions, labeled and unlabeled versions and in three different color schemes: black and white, color, and light gray. The color scheme matches the fraction strips and use colors that are meant to show good contrast among themselves. Do note that there is a significant prevalence of color-blindness in the population, so don't rely on all students being able to differentiate the colors.
Suggested activity for comparing fractions: Photocopy the black and white version onto an overhead projection slide and another copy onto a piece of paper. Alternatively, you can use two pieces of paper and hold them up to the light for this activity. Use a pencil to represent the first fraction on the paper copy. Use a non-permanent overhead pen to represent the second fraction. Lay the slide over the paper and compare the two circles. You should easily be able to tell which is greater or lesser or if the two fractions are equal. Re-use both sheets by erasing the pencil and washing off the marker.
Adding fractions with fraction circles will involve two copies on paper. Cut out the fraction circles and segments of one copy and leave the other copy intact. To add 1/3 + 1/2, for example, place a 1/3 segment and a 1/2 segment into a circle and hold it over various fractions on the intact copy to see what 1/2 + 1/3 is equivalent to. 5/6 or 10/12 should work.
Fraction Strips
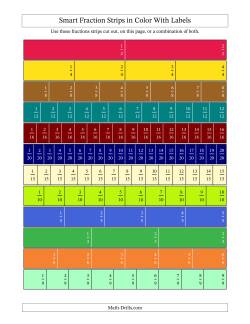
Fractions strips are often used for comparing fractions. Students are able to see quite easily the relationships and equivalence between fractions with different denominators. It can be quite useful for students to have two copies: one copy cut into strips and the other copy kept intact. They can then use the cut-out strips on the intact page to individually compare fractions. For example, they can use the halves strip to see what other fractions are equivalent to one-half. This can also be accomplished with a straight edge such as a ruler without cutting out any strips. Pairs or groups of strips can also be compared side-by-side if they are cut out. Addition and subtraction (etc.) are also possibilities; for example, adding a one-quarter and one-third can be accomplished by shifting the thirds strip so that it starts at the end of one-quarter then finding a strip that matches the end of the one-third mark (7/12 should do it).
Teachers might consider copying the fraction strips onto overhead projection acetates for whole class or group activities. Acetate versions are also useful as a hands-on manipulative for students in conjunction with an uncut page.
The "Smart" Fraction Strips include strips in a more useful order, eliminate the 7ths and 11ths strips as they don't have any equivalents and include 15ths and 16ths. The colors are consistent with the classic versions, so the two sets can be combined.
Modeling fractions

Fractions can represent parts of a group or parts of a whole. In these worksheets, fractions are modeled as parts of a group. Besides using the worksheets in this section, you can also try some more interesting ways of modeling fractions. Healthy snacks can make great models for fractions. Can you cut a cucumber into thirds? A tomato into quarters? Can you make two-thirds of the grapes red and one-third green?
-
Coloring Groups of Shapes to Represent Fractions Identifying Fractions from Colored Groups of Shapes (Only Simplified Fractions up to Eighths) Identifying Fractions from Colored Groups of Shapes (Halves Only) Identifying Fractions from Colored Groups of Shapes (Halves and Thirds) Identifying Fractions from Colored Groups of Shapes (Halves, Thirds and Fourths) Identifying Fractions from Colored Groups of Shapes (Up to Fifths) Identifying Fractions from Colored Groups of Shapes (Up to Sixths) Identifying Fractions from Colored Groups of Shapes (Up to Eighths) Identifying Fractions from Colored Groups of Shapes (OLD Version; Print Too Light)
-
Modeling Halves, Thirds and Fourths Coloring Halves, Thirds and Fourths Modeling Halves, Thirds, Fourths, and Fifths Coloring Halves, Thirds, Fourths, and Fifths Modeling Halves to Sixths Coloring Halves to Sixths Modeling Halves to Eighths Coloring Halves to Eighths Modeling Halves to Twelfths Coloring Halves to Twelfths
Ratio and Proportion Worksheets

The equivalent fractions models worksheets include only the "baking fractions" in the A versions. To see more difficult and varied fractions, please choose the B to J versions after loading the A version. More picture ratios can be found on holiday and seasonal pages. Try searching for picture ratios to find more.
-
Equivalent Fractions With Blanks (Multiply Right) ✎ Equivalent Fractions With Blanks (Divide Left) ✎ Equivalent Fractions With Blanks (Multiply Right or Divide Left) ✎ Equivalent Fractions With Blanks (Divide Right) ✎ Equivalent Fractions With Blanks (Multiply Left) ✎ Equivalent Fractions With Blanks (Multiply Left or Divide Right) ✎ Equivalent Fractions With Blanks (Multiply or Divide Right) ✎ Equivalent Fractions With Blanks (Multiply or Divide Left) ✎ Equivalent Fractions With Blanks (Multiply or Divide in Either Direction) ✎ Are These Fractions Equivalent? (Multiplier 2 to 5) Are These Fractions Equivalent? (Multiplier 5 to 15) Equivalent Fractions Models Equivalent Fractions Models with the Simplified Fraction First Equivalent Fractions Models with the Simplified Fraction Second
Comparing and Ordering Fractions

Comparing fractions involves deciding which of two fractions is greater in value or if the two fractions are equal in value. There are generally four methods that can be used for comparing fractions. First is to use common denominators. If both fractions have the same denominator, comparing the fractions simply involves comparing the numerators. Equivalent fractions can be used to convert one or both fractions, so they have common denominators. A second method is to convert both fractions to a decimal and compare the decimal numbers. Visualization is the third method. Using something like fraction strips, two fractions can be compared with a visual tool. The fourth method is to use a cross-multiplication strategy where the numerator of the first fraction is multiplied by the denominator of the second fraction; then the numerator of the second fraction is multiplied by the denominator of the first fraction. The resulting products can be compared to decide which fraction is greater (or if they are equal).
The worksheets in this section also include improper fractions. This might make the task of comparing even easier for some questions that involve both a proper and an improper fraction. If students recognize one fraction is greater than one and the other fraction is less than one, the greater fraction will be obvious.
-
Comparing Proper and Improper Fractions to Sixths ✎ Comparing Proper and Improper Fractions to Ninths (No Sevenths) ✎ Comparing Proper and Improper Fractions to Ninths ✎ Comparing Proper and Improper Fractions to Twelfths (No Sevenths; No Elevenths) ✎ Comparing Proper and Improper Fractions to Twelfths ✎ Comparing Improper Fractions to Sixths ✎ Comparing Improper Fractions to Ninths (No Sevenths) ✎ Comparing Improper Fractions to Ninths ✎ Comparing Improper Fractions to Twelfths (No Sevenths; No Elevenths) ✎ Comparing Improper Fractions to Twelfths ✎
This section additionally includes mixed fractions. When comparing mixed and improper fractions, it is useful to convert one of the fractions to the other's form either in writing or mentally. Converting to a mixed fraction is probably the better route since the first step is to compare the whole number portions, and if one is greater than the other, the proper fraction portion can be ignored. If the whole number portions are equal, the proper fractions must be compared to see which number is greater.
-
Comparing Proper, Improper and Mixed Fractions to Sixths ✎ Comparing Proper, Improper and Mixed Fractions to Ninths (No Sevenths) ✎ Comparing Proper, Improper and Mixed Fractions to Ninths ✎ Comparing Proper, Improper and Mixed Fractions to Twelfths (No Sevenths; No Elevenths) ✎ Comparing Proper, Improper and Mixed Fractions to Twelfths ✎
-
Comparing Improper and Mixed Fractions to Sixths ✎ Comparing Improper and Mixed Fractions to Ninths (No Sevenths) ✎ Comparing Improper and Mixed Fractions to Ninths ✎ Comparing Improper and Mixed Fractions to Twelfths (No Sevenths; No Elevenths) ✎ Comparing Improper and Mixed Fractions to Twelfths ✎
Many of the same strategies that work for comparing fractions also work for ordering fractions. Using manipulatives such as fraction strips, using number lines, or finding decimal equivalents will all have your student(s) putting fractions in the correct order in no time. We've probably said this before, but make sure that you emphasize that when comparing or ordering fractions, students understand that the whole needs to be the same. Comparing half the population of Canada with a third of the population of the United States won't cut it. Try using some visuals to reinforce this important concept. Even though we've included number lines below, feel free to use your own strategies.
-
Ordering Fractions with Easy Denominators to 10 + Negatives on a Number Line Ordering Fractions with Easy Denominators to 24 + Negatives on a Number Line Ordering Fractions with Easy Denominators to 60 + Negatives on a Number Line Ordering Fractions with Easy Denominators to 100 + Negatives on a Number Line
-
Ordering Fractions with All Denominators to 10 + Negatives on a Number Line Ordering Fractions with All Denominators to 24 + Negatives on a Number Line Ordering Fractions with All Denominators to 60 + Negatives on a Number Line Ordering Fractions with All Denominators to 100 + Negatives on a Number Line
The ordering fractions worksheets in this section do not include a number line, to allow for students to use various sorting strategies.
-
Ordering Positive Fractions with Like Denominators Ordering Positive Fractions with Like Numerators Ordering Positive Fractions with Like Numerators or Denominators Ordering Positive Fractions with Proper Fractions Only Ordering Positive Fractions with Improper Fractions Ordering Positive Fractions with Mixed Fractions Ordering Positive Fractions with Improper and Mixed Fractions
-
Ordering Positive and Negative Fractions with Like Denominators Ordering Positive and Negative Fractions with Like Numerators Ordering Positive and Negative Fractions with Like Numerators or Denominators Ordering Positive and Negative Fractions with Proper Fractions Only Ordering Positive and Negative Fractions with Improper Fractions Ordering Positive and Negative Fractions with Mixed Fractions Ordering Positive and Negative Fractions with Improper and Mixed Fractions
Simplifying & Converting Fractions Worksheets

Rounding fractions helps students to understand fractions a little better and can be applied to estimating answers to fractions questions. For example, if one had to estimate 1 4/7 × 6, they could probably say the answer was about 9 since 1 4/7 is about 1 1/2 and 1 1/2 × 6 is 9.
Learning how to simplify fractions makes a student's life much easier later on when learning operations with fractions. It also helps them to learn that different-looking fractions can be equivalent. One way of demonstrating this is to divide out two equivalent fractions. For example 3/2 and 6/4 both result in a quotient of 1.5 when divided. By practicing simplifying fractions, students will hopefully recognize unsimplified fractions when they start adding, subtracting, multiplying and dividing with fractions.
-
Converting Fractions to Decimals, Percents and Part-to-Part Ratios (Terminating Decimals Only) Converting Fractions to Decimals, Percents and Part-to-Whole Ratios (Terminating Decimals Only) Converting Decimals to Fractions, Percents and Part-to-Part Ratios (Terminating Decimals Only) Converting Decimals to Fractions, Percents and Part-to-Whole Ratios (Terminating Decimals Only) Converting Percents to Fractions, Decimals and Part-to-Part Ratios (Terminating Decimals Only) Converting Percents to Fractions, Decimals and Part-to-Whole Ratios (Terminating Decimals Only) Converting Part-to-Part Ratios to Fractions, Decimals and Percents (Terminating Decimals Only) Converting Part-to-Whole Ratios to Fractions, Decimals and Percents (Terminating Decimals Only) Converting Various Fractions, Decimals, Percents and Part-to-Part Ratios (Terminating Decimals Only) Converting Various Fractions, Decimals, Percents and Part-to-Whole Ratios (Terminating Decimals Only)
-
Converting Fractions to Decimals, Percents and Part-to-Part Ratios Converting Fractions to Decimals, Percents and Part-to-Whole Ratios Converting Decimals to Fractions, Percents and Part-to-Part Ratios Converting Decimals to Fractions, Percents and Part-to-Whole Ratios Converting Percents to Fractions, Decimals and Part-to-Part Ratios Converting Percents to Fractions, Decimals and Part-to-Whole Ratios Converting Part-to-Part Ratios to Fractions, Decimals and Percents Converting Part-to-Whole Ratios to Fractions, Decimals and Percents Converting Various Fractions, Decimals, Percents and Part-to-Part Ratios Converting Various Fractions, Decimals, Percents and Part-to-Whole Ratios Converting Various Fractions, Decimals, Percents and Part-to-Part Ratios with 7ths and 11ths Converting Various Fractions, Decimals, Percents and Part-to-Whole Ratios with 7ths and 11ths
Multiplying Fractions

Multiplying fractions is usually less confusing operationally than any other operation and can be less confusing conceptually if approached in the right way. The algorithm for multiplying is simply multiply the numerators then multiply the denominators. The magic word in understanding the multiplication of fractions is, "of." For example what is two-thirds OF six? What is a third OF a half? When you use the word, "of," it gets much easier to visualize fractions multiplication. Example: cut a loaf of bread in half, then cut the half into thirds. One third OF a half loaf of bread is the same as 1/3 x 1/2 and tastes delicious with butter.
-
Multiplying Two Proper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying Two Proper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ ✎ Multiplying Two Proper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying Two Proper Fractions with No Simplifying (Printable Only) Multiplying Two Proper Fractions with All Simplifying (Printable Only) Multiplying Two Proper Fractions with Some Simplifying (Printable Only)
-
Multiplying Proper and Improper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying Proper and Improper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying Proper and Improper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying Proper and Improper Fractions with No Simplifying (Printable Only) Multiplying Proper and Improper Fractions with All Simplifying (Printable Only) Multiplying Proper and Improper Fractions with Some Simplifying (Printable Only)
-
Multiplying Two Improper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying Two Improper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying Two Improper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying Two Improper Fractions with No Simplifying (Printable Only) Multiplying Two Improper Fractions with All Simplifying (Printable Only) Multiplying Two Improper Fractions with Some Simplifying (Printable Only)
-
Multiplying Proper and Mixed Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying Proper and Mixed Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying Proper and Mixed Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying Proper and Mixed Fractions with No Simplifying (Printable Only) Multiplying Proper and Mixed Fractions with All Simplifying (Printable Only) Multiplying Proper and Mixed Fractions with Some Simplifying (Printable Only)
-
Multiplying Two Mixed Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying Two Mixed Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying Two Mixed Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying Two Mixed Fractions with No Simplifying (Printable Only) Multiplying Two Mixed Fractions with All Simplifying (Printable Only) Multiplying Two Mixed Fractions with Some Simplifying (Printable Only)
-
Multiplying Whole Numbers and Proper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying Whole Numbers and Proper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying Whole Numbers and Proper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying Whole Numbers and Proper Fractions with No Simplifying (Printable Only) Multiplying Whole Numbers and Proper Fractions with All Simplifying (Printable Only) Multiplying Whole Numbers and Proper Fractions with Some Simplifying (Printable Only)
-
Multiplying Whole Numbers and Improper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying Whole Numbers and Improper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying Whole Numbers and Improper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying Whole Numbers and Improper Fractions with No Simplifying (Printable Only) Multiplying Whole Numbers and Improper Fractions with All Simplifying (Printable Only) Multiplying Whole Numbers and Improper Fractions with Some Simplifying (Printable Only)
-
Multiplying Whole Numbers and Mixed Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying Whole Numbers and Mixed Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying Whole Numbers and Mixed Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying Whole Numbers and Mixed Fractions with No Simplifying (Printable Only) Multiplying Whole Numbers and Mixed Fractions with All Simplifying (Printable Only) Multiplying Whole Numbers and Mixed Fractions with Some Simplifying (Printable Only)
-
Multiplying Proper, Improper and Mixed Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying Proper, Improper and Mixed Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying Proper, Improper and Mixed Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying Proper, Improper and Mixed Fractions with No Simplifying (Printable Only) Multiplying Proper, Improper and Mixed Fractions with All Simplifying (Printable Only) Multiplying Proper, Improper and Mixed Fractions with Some Simplifying (Printable Only)
-
Multiplying 3 Proper Fractions (Fillable, Savable, Printable) ✎ Multiplying 3 Proper and Improper Fractions (Fillable, Savable, Printable) ✎ Multiplying Proper and Improper Fractions and Whole Numbers (3 factors) (Fillable, Savable, Printable) ✎ Multiplying Fractions and Mixed Fractions (3 factors) (Fillable, Savable, Printable) ✎ Multiplying 3 Mixed Fractions (Fillable, Savable, Printable) ✎
Dividing Fractions

Conceptually, dividing fractions is probably the most difficult of all the operations, but we're going to help you out. The algorithm for dividing fractions is just like multiplying fractions, but you find the inverse of the second fraction or you cross-multiply. This gets you the right answer which is extremely important especially if you're building a bridge. We told you how to conceptualize fraction multiplication, but how does it work with division? Easy! You just need to learn the magic phrase: "How many ____'s are there in ______? For example, in the question 6 ÷ 1/2, you would ask, "How many halves are there in 6?" It becomes a little more difficult when both numbers are fractions, but it isn't a giant leap to figure it out. 1/2 ÷ 1/4 is a fairly easy example, especially if you think in terms of U.S. or Canadian coins. How many quarters are there in a half dollar?
-
Dividing Two Proper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Dividing Two Proper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Dividing Two Proper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Dividing Two Proper Fractions with No Simplifying (Printable Only) Dividing Two Proper Fractions with All Simplifying (Printable Only) Dividing Two Proper Fractions with Some Simplifying (Printable Only)
-
Dividing Proper and Improper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Dividing Proper and Improper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Dividing Proper and Improper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Dividing Proper and Improper Fractions with No Simplifying (Printable Only) Dividing Proper and Improper Fractions with All Simplifying (Printable Only) Dividing Proper and Improper Fractions with Some Simplifying (Printable Only)
-
Dividing Two Improper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Dividing Two Improper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Dividing Two Improper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Dividing Two Improper Fractions with No Simplifying (Printable Only) Dividing Two Improper Fractions with All Simplifying (Printable Only) Dividing Two Improper Fractions with Some Simplifying (Printable Only)
-
Dividing Proper and Mixed Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Dividing Proper and Mixed Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Dividing Proper and Mixed Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Dividing Proper and Mixed Fractions with No Simplifying (Printable Only) Dividing Proper and Mixed Fractions with All Simplifying (Printable Only) Dividing Proper and Mixed Fractions with Some Simplifying (Printable Only)
-
Dividing Two Mixed Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Dividing Two Mixed Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Dividing Two Mixed Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Dividing Two Mixed Fractions with No Simplifying (Printable Only) Dividing Two Mixed Fractions with All Simplifying (Printable Only) Dividing Two Mixed Fractions with Some Simplifying (Printable Only)
-
Dividing Whole Numbers and Proper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Dividing Whole Numbers and Proper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Dividing Whole Numbers and Proper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Dividing Whole Numbers and Proper Fractions with No Simplifying (Printable Only) Dividing Whole Numbers and Proper Fractions with All Simplifying (Printable Only) Dividing Whole Numbers and Proper Fractions with Some Simplifying (Printable Only)
-
Dividing Whole Numbers and Improper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Dividing Whole Numbers and Improper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Dividing Whole Numbers and Improper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Dividing Whole Numbers and Improper Fractions with No Simplifying (Printable Only) Dividing Whole Numbers and Improper Fractions with All Simplifying (Printable Only) Dividing Whole Numbers and Improper Fractions with Some Simplifying (Printable Only)
-
Dividing Whole Numbers and Mixed Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Dividing Whole Numbers and Mixed Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Dividing Whole Numbers and Mixed Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Dividing Whole Numbers and Mixed Fractions with No Simplifying (Printable Only) Dividing Whole Numbers and Mixed Fractions with All Simplifying (Printable Only) Dividing Whole Numbers and Mixed Fractions with Some Simplifying (Printable Only)
-
Dividing Proper, Improper and Mixed Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Dividing Proper, Improper and Mixed Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Dividing Proper, Improper and Mixed Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Dividing Proper, Improper and Mixed Fractions with No Simplifying (Printable Only) Dividing Proper, Improper and Mixed Fractions with All Simplifying (Printable Only) Dividing Proper, Improper and Mixed Fractions with Some Simplifying (Printable Only)
Multiplying and Dividing Fractions

This section includes worksheets with both multiplication and division mixed on each worksheet. Students will have to pay attention to the signs.
-
Multiplying and Dividing Two Proper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Two Proper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Two Proper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Two Proper Fractions with No Simplifying (Printable Only) Multiplying and Dividing Two Proper Fractions with All Simplifying (Printable Only) Multiplying and Dividing Two Proper Fractions with Some Simplifying (Printable Only)
-
Multiplying and Dividing Proper and Improper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Proper and Improper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Proper and Improper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Proper and Improper Fractions with No Simplifying (Printable Only) Multiplying and Dividing Proper and Improper Fractions with All Simplifying (Printable Only) Multiplying and Dividing Proper and Improper Fractions with Some Simplifying (Printable Only)
-
Multiplying and Dividing Two Improper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Two Improper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Two Improper Fractions (Fillable, Savable, Printable) ✎ Multiplying and Dividing Two Improper Fractions with No Simplifying (Printable Only) Multiplying and Dividing Two Improper Fractions with All Simplifying (Printable Only) Multiplying and Dividing Two Improper Fractions (Printable Only)
-
Multiplying and Dividing Proper and Mixed Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Proper and Mixed Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Proper and Mixed Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Proper and Mixed Fractions with No Simplifying (Printable Only) Multiplying and Dividing Proper and Mixed Fractions with All Simplifying (Printable Only) Multiplying and Dividing Proper and Mixed Fractions with Some Simplifying (Printable Only)
-
Multiplying and Dividing Two Mixed Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Two Mixed Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Two Mixed Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Two Mixed Fractions with No Simplifying (Printable Only) Multiplying and Dividing Two Mixed Fractions with All Simplifying (Printable Only) Multiplying and Dividing Two Mixed Fractions with Some Simplifying (Printable Only)
-
Multiplying and Dividing Whole Numbers and Proper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Whole Numbers and Proper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Whole Numbers and Proper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Whole Numbers and Proper Fractions with No Simplifying (Printable Only) Multiplying and Dividing Whole Numbers and Proper Fractions with All Simplifying (Printable Only) Multiplying and Dividing Whole Numbers and Proper Fractions with Some Simplifying (Printable Only)
-
Multiplying and Dividing Whole Numbers and Improper Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Whole Numbers and Improper Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Whole Numbers and Improper Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Whole Numbers and Improper Fractions with No Simplifying (Printable Only) Multiplying and Dividing Whole Numbers and Improper Fractions with All Simplifying (Printable Only) Multiplying and Dividing Whole Numbers and Improper Fractions with Some Simplifying (Printable Only)
-
Multiplying and Dividing Whole Numbers and Mixed Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Whole Numbers and Mixed Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Whole Numbers and Mixed Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Whole Numbers and Mixed Fractions with No Simplifying (Printable Only) Multiplying and Dividing Whole Numbers and Mixed Fractions with All Simplifying (Printable Only) Multiplying and Dividing Whole Numbers and Mixed Fractions with Some Simplifying (Printable Only)
-
Multiplying and Dividing Proper, Improper and Mixed Fractions with No Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Proper, Improper and Mixed Fractions with All Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Proper, Improper and Mixed Fractions with Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying and Dividing Proper, Improper and Mixed Fractions with No Simplifying (Printable Only) Multiplying and Dividing Proper, Improper and Mixed Fractions with All Simplifying (Printable Only) Multiplying and Dividing Proper, Improper and Mixed Fractions with Some Simplifying (Printable Only)
Adding Fractions

Adding fractions requires the annoying common denominator. Make it easy on your students by first teaching the concepts of equivalent fractions and least common multiples. Once students are familiar with those two concepts, the idea of finding fractions with common denominators for adding becomes that much easier. Spending time on modeling fractions will also help students to understand fractions addition. Relating fractions to familiar examples will certainly help. For example, if you add a 1/2 banana and a 1/2 banana, you get a whole banana. What happens if you add a 1/2 banana and 3/4 of another banana?
-
Adding Two Proper Fractions with Equal Denominators, Proper Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Equal Denominators, Proper Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Equal Denominators, Proper Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Equal Denominators, Proper Fractions Result, and No Simplifying (Printable Only) Adding Two Proper Fractions with Equal Denominators, Proper Fractions Result, and All Simplifying (Printable Only) Adding Two Proper Fractions with Equal Denominators, Proper Fractions Result, and Some Simplifying (Printable Only)
-
Adding Two Proper Fractions with Equal Denominators, Mixed Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Equal Denominators, Mixed Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Equal Denominators, Mixed Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Equal Denominators, Mixed Fractions Result, and No Simplifying (Printable Only) Adding Two Proper Fractions with Equal Denominators, Mixed Fractions Result, and All Simplifying (Printable Only) Adding Two Proper Fractions with Equal Denominators, Mixed Fractions Result, and Some Simplifying (Printable Only)
-
Adding Two Proper Fractions with Similar Denominators, Proper Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Similar Denominators, Proper Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Similar Denominators, Proper Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Similar Denominators, Proper Fractions Result, and No Simplifying (Printable Only) Adding Two Proper Fractions with Similar Denominators, Proper Fractions Result, and All Simplifying (Printable Only) Adding Two Proper Fractions with Similar Denominators, Proper Fractions Result, and Some Simplifying (Printable Only)
-
Adding Two Proper Fractions with Similar Denominators, Mixed Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Similar Denominators, Mixed Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Similar Denominators, Mixed Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Similar Denominators, Mixed Fractions Result, and No Simplifying (Printable Only) Adding Two Proper Fractions with Similar Denominators, Mixed Fractions Result, and All Simplifying (Printable Only) Adding Two Proper Fractions with Similar Denominators, Mixed Fractions Result, and Some Simplifying (Printable Only)
-
Adding Two Proper Fractions with Unlike Denominators, Proper Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Unlike Denominators, Proper Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Unlike Denominators, Proper Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Unlike Denominators, Proper Fractions Result, and No Simplifying (Printable Only) Adding Two Proper Fractions with Unlike Denominators, Proper Fractions Result, and All Simplifying (Printable Only) Adding Two Proper Fractions with Unlike Denominators, Proper Fractions Result, and Some Simplifying (Printable Only)
-
Adding Two Proper Fractions with Unlike Denominators, Mixed Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Unlike Denominators, Mixed Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Unlike Denominators, Mixed Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Adding Two Proper Fractions with Unlike Denominators, Mixed Fractions Result, and No Simplifying (Printable Only) Adding Two Proper Fractions with Unlike Denominators, Mixed Fractions Result, and All Simplifying (Printable Only) Adding Two Proper Fractions with Unlike Denominators, Mixed Fractions Result, and Some Simplifying (Printable Only)
-
Adding Proper and Improper Fractions with Equal Denominators and No Simplifying (Fillable, Savable, Printable) ✎ Adding Proper and Improper Fractions with Equal Denominators and All Simplifying (Fillable, Savable, Printable) ✎ Adding Proper and Improper Fractions with Equal Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ Adding Proper and Improper Fractions with Equal Denominators and No Simplifying (Printable Only) Adding Proper and Improper Fractions with Equal Denominators and All Simplifying (Printable Only) Adding Proper and Improper Fractions with Equal Denominators and Some Simplifying (Printable Only)
-
Adding Proper and Improper Fractions with Similar Denominators and No Simplifying (Fillable, Savable, Printable) ✎ Adding Proper and Improper Fractions with Similar Denominators and All Simplifying (Fillable, Savable, Printable) ✎ Adding Proper and Improper Fractions with Similar Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ Adding Proper and Improper Fractions with Similar Denominators and No Simplifying (Printable Only) Adding Proper and Improper Fractions with Similar Denominators and All Simplifying (Printable Only) Adding Proper and Improper Fractions with Similar Denominators and Some Simplifying (Printable Only)
-
Adding Proper and Improper Fractions with Unlike Denominators and No Simplifying (Fillable, Savable, Printable) ✎ Adding Proper and Improper Fractions with Unlike Denominators and All Simplifying (Fillable, Savable, Printable) ✎ Adding Proper and Improper Fractions with Unlike Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ Adding Proper and Improper Fractions with Unlike Denominators and No Simplifying (Printable Only) Adding Proper and Improper Fractions with Unlike Denominators and All Simplifying (Printable Only) Adding Proper and Improper Fractions with Unlike Denominators and Some Simplifying (Printable Only)
A common strategy to use when adding mixed fractions is to convert the mixed fractions to improper fractions, complete the addition, then switch back. Another strategy which requires a little less brainpower is to look at the whole numbers and fractions separately. Add the whole numbers first. Add the fractions second. If the resulting fraction is improper, then it needs to be converted to a mixed number. The whole number portion can be added to the original whole number portion.
-
Adding Two Mixed Fractions with Equal Denominators and No Simplifying (Fillable, Savable, Printable) ✎ Adding Two Mixed Fractions with Equal Denominators and All Simplifying (Fillable, Savable, Printable) ✎ Adding Two Mixed Fractions with Equal Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ Adding Two Mixed Fractions with Equal Denominators and No Simplifying (Printable Only) Adding Two Mixed Fractions with Equal Denominators and All Simplifying (Printable Only) Adding Two Mixed Fractions with Equal Denominators and Some Simplifying (Printable Only)
-
Adding Two Mixed Fractions with Similar Denominators and No Simplifying (Fillable, Savable, Printable) ✎ Adding Two Mixed Fractions with Similar Denominators and All Simplifying (Fillable, Savable, Printable) ✎ Adding Two Mixed Fractions with Similar Denominators and Some Simplifying Adding Two Mixed Fractions with Similar Denominators and No Simplifying (Printable Only) Adding Two Mixed Fractions with Similar Denominators and All Simplifying (Printable Only) Adding Two Mixed Fractions with Similar Denominators and Some Simplifying (Printable Only)
-
Adding Two Mixed Fractions with Unlike Denominators and No Simplifying (Fillable, Savable, Printable) ✎ Adding Two Mixed Fractions with Unlike Denominators and All Simplifying (Fillable, Savable, Printable) ✎ Adding Two Mixed Fractions with Unlike Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ Adding Two Mixed Fractions with Unlike Denominators and No Simplifying (Printable Only) Adding Two Mixed Fractions with Unlike Denominators and All Simplifying (Printable Only) Adding Two Mixed Fractions with Unlike Denominators and Some Simplifying (Printable Only)
Subtracting Fractions

There isn't a lot of difference between adding and subtracting fractions. Both require a common denominator which requires some prerequisite knowledge. The only difference is the second and subsequent numerators are subtracted from the first one. There is a danger that you might end up with a negative number when subtracting fractions, so students might need to learn what it means in that case. When it comes to any concept in fractions, it is always a good idea to relate it to a familiar or easy-to-understand situation. For example, 7/8 - 3/4 = 1/8 could be given meaning in the context of a race. The first runner was 7/8 around the track when the second runner was 3/4 around the track. How far ahead was the first runner? (1/8 of the track).
-
Subtracting Two Proper Fractions with Equal Denominators, Proper Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Two Proper Fractions with Equal Denominators, Proper Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Subtracting Two Proper Fractions with Equal Denominators, Proper Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Two Proper Fractions with Equal Denominators, Proper Fractions Results, and No Simplifying (Printable Only) Subtracting Two Proper Fractions with Equal Denominators, Proper Fractions Results, and All Simplifying (Printable Only) Subtracting Two Proper Fractions with Equal Denominators, Proper Fractions Results, and Some Simplifying (Printable Only)
-
Subtracting Two Proper Fractions with Similar Denominators, Proper Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Two Proper Fractions with Similar Denominators, Proper Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Subtracting Two Proper Fractions with Similar Denominators, Proper Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Two Proper Fractions with Similar Denominators, Proper Fractions Results, and No Simplifying (Printable Only) Subtracting Two Proper Fractions with Similar Denominators, Proper Fractions Results, and All Simplifying (Printable Only) Subtracting Two Proper Fractions with Similar Denominators, Proper Fractions Results, and Some Simplifying (Printable Only)
-
Subtracting Two Proper Fractions with Unlike Denominators, Proper Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Two Proper Fractions with Unlike Denominators, Proper Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Subtracting Two Proper Fractions with Unlike Denominators, Proper Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Two Proper Fractions with Unlike Denominators, Proper Fractions Results, and No Simplifying (Printable Only) Subtracting Two Proper Fractions with Unlike Denominators, Proper Fractions Results, and All Simplifying (Printable Only) Subtracting Two Proper Fractions with Unlike Denominators, Proper Fractions Results, and Some Simplifying (Printable Only)
-
Subtracting Proper and Improper Fractions with Equal Denominators, Proper Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Equal Denominators, Proper Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Equal Denominators, Proper Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Equal Denominators, Proper Fractions Results, and No Simplifying (Printable Only) Subtracting Proper and Improper Fractions with Equal Denominators, Proper Fractions Results, and All Simplifying (Printable Only) Subtracting Proper and Improper Fractions with Equal Denominators, Proper Fractions Results, and Some Simplifying (Printable Only)
-
Subtracting Proper and Improper Fractions with Similar Denominators, Proper Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Similar Denominators, Proper Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Similar Denominators, Proper Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Similar Denominators, Proper Fractions Results, and No Simplifying (Printable Only) Subtracting Proper and Improper Fractions with Similar Denominators, Proper Fractions Results, and All Simplifying (Printable Only) Subtracting Proper and Improper Fractions with Similar Denominators, Proper Fractions Results, and Some Simplifying (Printable Only)
-
Subtracting Proper and Improper Fractions with Unlike Denominators, Proper Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Unlike Denominators, Proper Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Unlike Denominators, Proper Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Unlike Denominators, Proper Fractions Results, and No Simplifying (Printable Only) Subtracting Proper and Improper Fractions with Unlike Denominators, Proper Fractions Results, and All Simplifying (Printable Only) Subtracting Proper and Improper Fractions with Unlike Denominators, Proper Fractions Results, and Some Simplifying (Printable Only)
-
Subtracting Proper and Improper Fractions with Equal Denominators, Mixed Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Equal Denominators, Mixed Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Equal Denominators, Mixed Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Equal Denominators, Mixed Fractions Results, and No Simplifying (Printable Only) Subtracting Proper and Improper Fractions with Equal Denominators, Mixed Fractions Results, and All Simplifying (Printable Only) Subtracting Proper and Improper Fractions with Equal Denominators, Mixed Fractions Results, and Some Simplifying (Printable Only)
-
Subtracting Proper and Improper Fractions with Similar Denominators, Mixed Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Similar Denominators, Mixed Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Similar Denominators, Mixed Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Similar Denominators, Mixed Fractions Results, and No Simplifying (Printable Only) Subtracting Proper and Improper Fractions with Similar Denominators, Mixed Fractions Results, and All Simplifying (Printable Only) Subtracting Proper and Improper Fractions with Similar Denominators, Mixed Fractions Results, and Some Simplifying (Printable Only)
-
Subtracting Proper and Improper Fractions with Unlike Denominators, Mixed Fractions Results, and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Unlike Denominators, Mixed Fractions Results, and All Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Unlike Denominators, Mixed Fractions Results, and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Proper and Improper Fractions with Unlike Denominators, Mixed Fractions Results, and No Simplifying (Printable Only) Subtracting Proper and Improper Fractions with Unlike Denominators, Mixed Fractions Results, and All Simplifying (Printable Only) Subtracting Proper and Improper Fractions with Unlike Denominators, Mixed Fractions Results, and Some Simplifying (Printable Only)
-
Subtracting Mixed Fractions with Equal Denominators, and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Mixed Fractions with Equal Denominators, and All Simplifying (Fillable, Savable, Printable) ✎ Subtracting Mixed Fractions with Equal Denominators, and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Mixed Fractions with Equal Denominators, and No Simplifying (Printable Only) Subtracting Mixed Fractions with Equal Denominators, and All Simplifying (Printable Only) Subtracting Mixed Fractions with Equal Denominators, and Some Simplifying (Printable Only)
-
Subtracting Mixed Fractions with Similar Denominators, and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Mixed Fractions with Similar Denominators, and All Simplifying (Fillable, Savable, Printable) ✎ Subtracting Mixed Fractions with Similar Denominators, and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Mixed Fractions with Similar Denominators, and No Simplifying (Printable Only) Subtracting Mixed Fractions with Similar Denominators, and All Simplifying (Printable Only) Subtracting Mixed Fractions with Similar Denominators, and Some Simplifying (Printable Only)
-
Subtracting Mixed Fractions with Unlike Denominators, and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Mixed Fractions with Unlike Denominators, and All Simplifying (Fillable, Savable, Printable) ✎ Subtracting Mixed Fractions with Unlike Denominators, and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Mixed Fractions with Unlike Denominators, and No Simplifying (Printable Only) Subtracting Mixed Fractions with Unlike Denominators, and All Simplifying (Printable Only) Subtracting Mixed Fractions with Unlike Denominators, and Some Simplifying (Printable Only)
Adding and Subtracting Fractions

Mixing up the signs on operations with fractions worksheets makes students pay more attention to what they are doing and allows for a good test of their skills in more than one operation.
-
Adding and Subtracting Proper and Improper Fractions with Equal Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ Adding and Subtracting Proper and Improper Fractions with Similar Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ Adding and Subtracting Proper and Improper Fractions with Unlike Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ Adding and Subtracting Proper and Improper Fractions with Equal Denominators and Some Simplifying (Printable Only) Adding and Subtracting Proper and Improper Fractions with Similar Denominators and Some Simplifying (Printable Only) Adding and Subtracting Proper and Improper Fractions with Unlike Denominators and Some Simplifying (Printable Only)
-
Adding and Subtracting Mixed Fractions with Equal Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ Adding and Subtracting Mixed Fractions with Similar Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ Adding and Subtracting Mixed Fractions with Unlike Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ Adding and Subtracting Mixed Fractions with Equal Denominators and Some Simplifying (Printable Only) Adding and Subtracting Mixed Fractions with Similar Denominators and Some Simplifying (Printable Only) Adding and Subtracting Mixed Fractions with Unlike Denominators and Some Simplifying (Printable Only) Adding/Subtracting Three Fractions/Mixed Fractions
All Operations Fractions Worksheets

-
All Operations with Two Proper Fractions with Equal Denominators, Proper Fractions Results and No Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Proper Fractions with Equal Denominators, Proper Fractions Results and All Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Proper Fractions with Equal Denominators, Proper Fractions Results and Some Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Proper Fractions with Equal Denominators, Proper Fractions Results and No Simplifying (Printable Only) All Operations with Two Proper Fractions with Equal Denominators, Proper Fractions Results and All Simplifying (Printable Only) All Operations with Two Proper Fractions with Equal Denominators, Proper Fractions Results and Some Simplifying (Printable Only)
-
All Operations with Two Proper Fractions with Similar Denominators, Proper Fractions Results and No Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Proper Fractions with Similar Denominators, Proper Fractions Results and All Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Proper Fractions with Similar Denominators, Proper Fractions Results and Some Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Proper Fractions with Similar Denominators, Proper Fractions Results and No Simplifying (Printable Only) All Operations with Two Proper Fractions with Similar Denominators, Proper Fractions Results and All Simplifying (Printable Only) All Operations with Two Proper Fractions with Similar Denominators, Proper Fractions Results and Some Simplifying (Printable Only)
-
All Operations with Two Proper Fractions with Unlike Denominators, Proper Fractions Results and No Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Proper Fractions with Unlike Denominators, Proper Fractions Results and All Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Proper Fractions with Unlike Denominators, Proper Fractions Results and Some Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Proper Fractions with Unlike Denominators, Proper Fractions Results and No Simplifying (Printable Only) All Operations with Two Proper Fractions with Unlike Denominators, Proper Fractions Results and All Simplifying (Printable Only) All Operations with Two Proper Fractions with Unlike Denominators, Mixed Fractions Results and Some Simplifying (Printable Only)
-
All Operations with Proper and Improper Fractions with Equal Denominators and No Simplifying (Fillable, Savable, Printable) ✎ All Operations with Proper and Improper Fractions with Equal Denominators and All Simplifying (Fillable, Savable, Printable) ✎ All Operations with Proper and Improper Fractions with Equal Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ All Operations with Proper and Improper Fractions with Equal Denominators and No Simplifying (Printable Only) All Operations with Proper and Improper Fractions with Equal Denominators and All Simplifying (Printable Only) All Operations with Proper and Improper Fractions with Equal Denominators and Some Simplifying (Printable Only)
-
All Operations with Proper and Improper Fractions with Similar Denominators and No Simplifying (Fillable, Savable, Printable) ✎ All Operations with Proper and Improper Fractions with Similar Denominators and All Simplifying (Fillable, Savable, Printable) ✎ All Operations with Proper and Improper Fractions with Similar Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ All Operations with Proper and Improper Fractions with Similar Denominators and No Simplifying (Printable Only) All Operations with Proper and Improper Fractions with Similar Denominators and All Simplifying (Printable Only) All Operations with Proper and Improper Fractions with Similar Denominators and Some Simplifying (Printable Only)
-
All Operations with Proper and Improper Fractions with Unlike Denominators and No Simplifying (Fillable, Savable, Printable) ✎ All Operations with Proper and Improper Fractions with Unlike Denominators and All Simplifying (Fillable, Savable, Printable) ✎ All Operations with Proper and Improper Fractions with Unlike Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ All Operations with Proper and Improper Fractions with Unlike Denominators and No Simplifying (Printable Only) All Operations with Proper and Improper Fractions with Unlike Denominators and All Simplifying (Printable Only) All Operations with Proper and Improper Fractions with Unlike Denominators and Some Simplifying (Printable Only)
-
All Operations with Two Mixed Fractions with Equal Denominators and No Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Mixed Fractions with Equal Denominators and All Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Mixed Fractions with Equal Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Mixed Fractions with Equal Denominators and No Simplifying (Printable Only) All Operations with Two Mixed Fractions with Equal Denominators and All Simplifying (Printable Only) All Operations with Two Mixed Fractions with Equal Denominators and Some Simplifying (Printable Only)
-
All Operations with Two Mixed Fractions with Similar Denominators and No Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Mixed Fractions with Similar Denominators and All Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Mixed Fractions with Similar Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Mixed Fractions with Similar Denominators and No Simplifying (Printable Only) All Operations with Two Mixed Fractions with Similar Denominators and All Simplifying (Printable Only) All Operations with Two Mixed Fractions with Similar Denominators and Some Simplifying (Printable Only)
-
All Operations with Two Mixed Fractions with Unlike Denominators and No Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Mixed Fractions with Unlike Denominators and All Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Mixed Fractions with Unlike Denominators and Some Simplifying (Fillable, Savable, Printable) ✎ All Operations with Two Mixed Fractions with Unlike Denominators and No Simplifying (Printable Only) All Operations with Two Mixed Fractions with Unlike Denominators and All Simplifying (Printable Only) All Operations with Two Mixed Fractions with Unlike Denominators and Some Simplifying (Printable Only)
Operations with Negative Fractions Worksheets

Although some of these worksheets are single operations, it should be helpful to have all of these in the same location. There are some special considerations when completing operations with negative fractions. It is usually very helpful to change any mixed numbers to an improper fraction before proceeding. It is important to pay attention to the signs and know the rules for multiplying positives and negatives (++ = +, +- = -, -+ = - and -- = +).
-
Adding Negative Proper Fractions with Unlike Denominators Up to Sixths, Proper Fractions Results and Some Simplifying (Fillable, Savable, Printable) ✎ Adding Negative Proper Fractions with Unlike Denominators Up to Twelfths, Proper Fractions Results and Some Simplifying (Fillable, Savable, Printable) ✎ Adding Negative Mixed Fractions with Unlike Denominators Up to Sixths, Proper Fractions Results and No Simplifying (Fillable, Savable, Printable) ✎ Adding Negative Mixed Fractions with Unlike Denominators Up to Twelfths, Proper Fractions Results and No Simplifying (Fillable, Savable, Printable) ✎ Adding Negative Proper Fractions with Denominators Up to Sixths, Proper Fraction Results and Some Simplifying (Printable Only) Adding Negative Proper Fractions with Denominators Up to Twelfths, Proper Fraction Results and Some Simplifying (Printable Only) Adding Negative Mixed Fractions with Denominators Up to Sixths and Some Simplifying (Printable Only) Adding Negative Mixed Fractions with Denominators Up to Twelfths and Some Simplifying (Printable Only)
-
Subtracting Negative Proper Fractions with Unlike Denominators Up to Sixths, Proper Fractions Results and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Negative Proper Fractions with Unlike Denominators Up to Twelfths, Proper Fractions Results and Some Simplifying (Fillable, Savable, Printable) ✎ Subtracting Negative Mixed Fractions with Unlike Denominators Up to Sixths, Mixed Fractions Results and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Negative Mixed Fractions with Unlike Denominators Up to Twelfths, Mixed Fractions Results and No Simplifying (Fillable, Savable, Printable) ✎ Subtracting Negative Proper Fractions with Denominators Up to Sixths, Proper Fraction Results and Some Simplifying (Printable Only) Subtracting Negative Proper Fractions with Denominators Up to Twelfths, Proper Fraction Results and Some Simplifying (Printable Only) Subtracting Negative Mixed Fractions with Denominators Up to Sixths and Some Simplifying (Printable Only) Subtracting Negative Mixed Fractions with Denominators Up to Twelfths and Some Simplifying (Printable Only)
-
Multiplying Negative Proper Fractions with Denominators Up to Sixths, Proper Fractions Results and Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying Negative Proper Fractions with Denominators Up to Twelfths, Proper Fractions Results and Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying Negative Mixed Fractions with Denominators Up to Sixths, Proper Fractions Results and Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying Negative Mixed Fractions with Denominators Up to Twelfths, Proper Fractions Results and Some Simplifying (Fillable, Savable, Printable) ✎ Multiplying Negative Proper Fractions with Denominators Up to Sixths, Proper Fraction Results and Some Simplifying (Printable Only) Multiplying Negative Proper Fractions with Denominators Up to Twelfths, Proper Fraction Results and Some Simplifying (Printable Only) Multiplying Negative Mixed Fractions with Denominators Up to Sixths and Some Simplifying (Printable Only) Multiplying Negative Mixed Fractions with Denominators Up to Twelfths and Some Simplifying (Printable Only)
-
Dividing Negative Proper Fractions with Denominators Up to Sixths, Mixed Fractions Results and Some Simplifying (Fillable, Savable, Printable) ✎ Dividing Negative Proper Fractions with Denominators Up to Twelfths, Mixed Fractions Results and Some Simplifying (Fillable, Savable, Printable) ✎ Dividing Negative Mixed Fractions with Denominators Up to Twelfths, Mixed Fractions Results and No Simplifying (Fillable, Savable, Printable) ✎ Dividing Negative Mixed Fractions with Denominators Up to Twelfths, Mixed Fractions Results and No Simplifying (Fillable, Savable, Printable) ✎ Dividing Negative Proper Fractions with Denominators Up to Sixths, Proper Fraction Results and Some Simplifying (Printable Only) Dividing Negative Proper Fractions with Denominators Up to Twelfths, Proper Fraction Results and Some Simplifying (Printable Only) Dividing Negative Mixed Fractions with Denominators Up to Sixths and Some Simplifying (Printable Only) Dividing Negative Mixed Fractions with Denominators Up to Twelfths and Some Simplifying (Printable Only)
Order of Operations with Fractions Worksheets

The order of operations worksheets in this section actually reside on the Order of Operations page, but they are included here for your convenience.
-
2-Step Order of Operations with Positive & Negative Fractions 3-Step Order of Operations with Positive & Negative Fractions 4-Step Order of Operations with Positive & Negative Fractions 5-Step Order of Operations with Positive & Negative Fractions 6-Step Order of Operations with Positive & Negative Fractions
